MEMS-Based Deformable Mirrors

- Aluminum-, Protected Silver-, or Gold-Coated MEMS-Based Deformable Mirrors
- 12 x 12 Actuator Array (140 Active)
- Mirror 3 dB Bandwidth of ~3.5 kHz
DM140A-35-UM01
12 x 12 Actuator Array
Ø2" x 0.89" Housing
MEMS Deformable Mirror Schematic

Please Wait
Features
- Multi-DM: 12 x 12 Actuator Array (140 Active)
- 3.5 μm Maximum Actuator Displacement
- Zero Hysteresis
- Sub-Nanometer Repeatability (Average Step Size <1 nm)
- Low Inter-Actuator Coupling of ~13% Results in High Spatial Resolution
- Aluminum-, Protected Silver-, or Gold-Coated Mirrors Available (See Graphs Tab)
- Protective Window with 6° Wedge and Broadband Antireflection Coating for 400 - 1100 nm
- 1020 (Kilo-DM) Actuator Model Available Through Boston Micromachines Corporation
Through our partnership with Boston Micromachines Corporation (BMC), Thorlabs is pleased to offer BMC's Multi-DM micromachined deformable mirror systems for advanced optical control. To facilitate installation and setup, each package includes the deformable mirror, driver, and control software. These mirrors are capable of changing shape in order to correct a highly distorted incident wavefront (refer to theTypes of Aberrations tab to learn more about the aberrations that a DM can correct). Micro-electro-mechanical (MEMS) deformable mirrors are currently the most widely used technology in wavefront shaping applications given their versatility, maturity of technology, and the high resolution wavefront correction that they afford.
These versatile DMs, which are fabricated using polysilicon surface micromachining fabrication methods, offer sophisticated aberration compensation in easy-to-use packages. The mirror consists of a membrane that is deformed by 140 electrostatic actuators (i.e., a 12 x 12 actuator array with four inactive corner actuators), each of which can be individually controlled. These actuators provide 3.5 μm stroke over a compact area. In addition, the Kilo-DM with 1020 actuators (i.e. a 32 x 32 actuator array with four inactive corner actuators) is available through Boston Micromachines Corporation. The Kilo-DM deformable mirror actuators provide 1.5 µm stroke. Unlike piezoelectric deformable mirrors, the electrostatic actuation used with BMC's mirrors ensures deformation without hysteresis.

Figure 1.3 DM Electrical Interface
The Multi-DM and Kilo-DM mirrors are available with either a gold-, protected silver-, or aluminum-coated mirror. The mirrors are protected by a 6° wedge that is AR coated for the 400 - 1100 nm range. Refer to the Graphs tab for coating curve information. If you have an interest in a different coating range, please contact Tech Support. Although the use of DMs in astronomy is well known, these miniature, precision wavefront control devices are also helping researchers in beam forming, microscopy, laser communication, and retinal imaging applications.
Adaptive Optics
The deformable mirror is one of the three main components that comprise an adaptive optics (AO) system. Such systems are used to correct (shape) the wavefront of a beam of light. Together with a wavefront sensor and control software, the DM forms a closed-loop system that is capable of actively correcting phase aberrations in real time (to learn more, please click on the AO Tutorial tab). Thorlabs offers CMOS-based Shack-Hartmann Wavefront Sensors.
Traditionally, these systems were used by the international astronomy and US defense communities, but they are a great addition to any field that would benefit from being able to control the phase of light. Today, the use of adaptive optics has permeated into a multitude of fields including femtosecond pulse shaping, microscopy, laser communication, vision correction, and retinal imaging.
| Adaptive Optics Kits | ||
|---|---|---|
 Click to Enlarge |
 Click to Enlarge |
|
| In an effort to bring adaptive optics to even more research fields, Thorlabs has partnered with Boston Micromachines Corporation (BMC) to provide adaptive optics kits that incorporate these MEMS-based deformable mirrors. These kits bundle the three primary components for any adaptive optics system: a MEMS deformable mirror system, a wavefront sensor, and real-time control software. In addition, the kits also include a light source, all collimation/imaging optics, and all necessary mounting hardware, except for a breadboard. These kits are specifically designed to provide an affordable, easy-to-use adaptive optics solution that can be integrated into a research system in hours instead of months. Kits with components other than those listed on their webpage can be ordered by contacting Tech Support. | ||
| Item # | DM140A-35-UP01 | DM140A-35-P01 | DM140A-35-UM01 | Kilo-3.5-DMa |
|---|---|---|---|---|
| Mirror Coating | Aluminum | Protected Silver | Gold | Aluminum, Protected Silver, or Gold |
| Actuator Array | 12 x 12 (140 Active)b | Ø34 (952 Active) | ||
| Actuator Stroke (Max)c | 3.5 µm | 3.5 µm | ||
| Actuator Pitch | 400 µm | 400 µm | ||
| Clear Aperture | 4.4 mm x 4.4 mm | Ø13.2 mm | ||
| Average Step Sized | <1 nm | <1 nm | ||
| Hysteresis | None | None | ||
| Fill Factore | >99% | >99% | ||
| Acceptance Angle | ±15° | ±45° | ||
| Mechanical Response Time (10% - 90%) | <75 μs (~13.3 kHz) | <80 μs (~12.5 kHz) | ||
| Surface Quality | <30 nm (RMS) | <30 nm (RMS) | ||
| Cable Length (from Mirror to Driver) | 60" | 2 m | ||
| Driver Specifications | ||||
| Frame Rate (Max) | 8 kHz | 34 kHz | ||
| Resolution | 14 Bit | 14 bit | ||
| Driver Dimensions | 9.0" x 7.0" x 2.5" (229 mm x 178 mm x 64 mm) |
19.0" x 18.5" x 5.25" (483 mm x 470 mm x 133 mm) |
||
| Computer Interface | USB 2.0 | PCIe Card | ||
Coating Curves
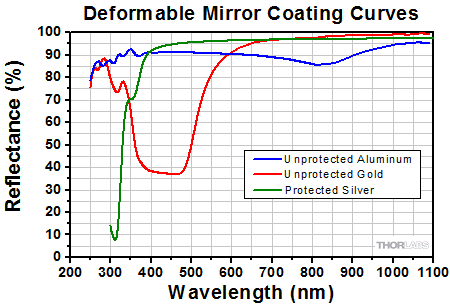
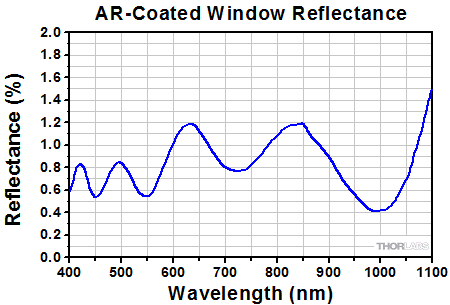
Depicted here are typical reflectance plots for aluminum-, protected silver-, and gold-coated surfaces (without the protective window) as well as the antireflection (AR) coating curve for the protective 6° wedged window. The data for the unprotected aluminum, protected silver, and gold coatings were obtained with using unpolarized light that was incident at 45°.
Click to Enlarge
Figure 3.1 Reflectance of the Metallic Mirror Coating
Click to Enlarge
Figure 3.2 Reflectance of the AR-Coated, 6° Wedged Window
Actuator Deflection
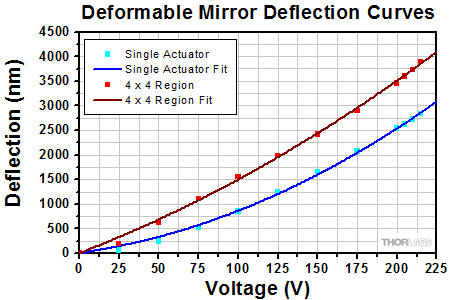
Figure 3.3 shows the typical deflection of a single actuator and a 4 x 4 region of actuators in the mirror as a function of the input voltage. This graph is included on the data sheet included with each deformable mirror. A polynomial fit has been applied to each set of points and the coefficients are provided on the data sheet for each mirror. Figure 3.4 shows the error in the mirror shape when compared to the shape defined by different Zernike coefficients for different peak-to-valley amplitudes of the wavefront distortion.
Click to Enlarge
Figure 3.3 Typical deflection of a single actuator and a 4 x 4 region of actuators as a function of voltage.
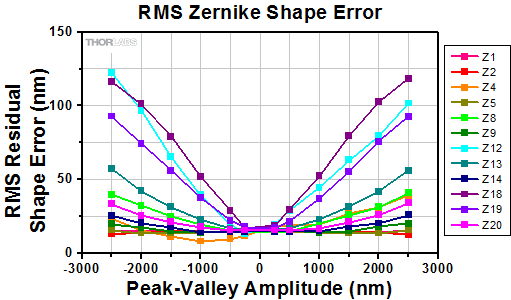
Click to Enlarge
Figure 3.4 Residual error of the mirror shape compared to different Zernike functions for a range of wavefront distortion amplitudes.
Ideally, an optical image-forming system will produce a unique image point for each object point. Any departures from this ideal theory of Gaussian (also known as paraxial or first-order) Optics are known as aberrations and can be categorized into two main types: monochromatic (single color) aberrations and chromatic (varying wavelength) aberrations. When aberrations are present, the peak intensity will be reduced and the image or laser beam propagating to a target will be blurred. Below, we will take a look at the seven primary types of aberrations, five of which are of the monochromatic variety and two of which are of the chromatic variety. Deformable mirrors are capable of removing all types of monochromatic aberrations from a wavefront to allow for the formation of an ideal, diffraction-limited image, even if optics without diffraction-limited performance are being used in the optical system.
Monochromatic Aberrations
There are five primary monochromatic aberrations, which can be further divided into two subgroups: those that deteriorate the image (spherical aberration, coma, and astigmatism) and those that deform the image (field curvature and distortion). These aberrations are a direct result of departures from first-order (i.e., sinθ≈θ) theory, which assumes the light rays make small angles with the principal axis. As soon as one wants to consider light rays incident on the periphery of a lens, the statement sinθ≈θ, which forms the basis of paraxial optics, is no longer satisfactory and one must consider more terms in the expansion:
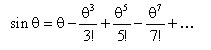
The five primary monochromatic aberrations were first studied by Ludwig von Seidel, and hence, they are frequently referred to as the Seidel aberrations. Please note that since the expansion of sinθ is an infinite sum, the five monochromatic aberrations discussed below are not the only ones possible; there are additional higher-order aberrations that make smaller contributions to image degradation. The surface of the deformable mirror can be altered to accommodate all of these types of monochromatic aberrations.
For parallel incoming light rays, an ideal lens will be able to focus the rays to a point on the optical axis as shown in Figure 4.1 (a) consequently, under ideal circumstances, the image of a point source that is located on the optical axis will be a bright circular disk surrounded by faint rings [see the Airy diffraction pattern shown in Figure 4.1 (b)]. However, in reality, the light rays that strike a spherical converging lens far from the principal axis will be focused to a point that is closer to the lens than those light rays that strike the spherical lens near the principal axis [see Figure 4.1 (c)]. Consequently, there is no single focus for a spherical lens, and the image will appear to be blurred; instead of having an Airy diffraction pattern in which nearly all the light is contained in a central bright circular spot, spherical aberration will redistribute some of the light from the central disk to the surrounding rings [see Figure 4.1 (d)], thereby reducing image contrast. Whenever spherical aberration is present, the best focus for an uncorrected lens will be somewhere between the focal planes of the peripheral and axial rays. Please note that spherical aberration only pertains to object points that are located on the optical axis.

Figure 4.1 Comparison of an ideal situation to one in which spherical aberration is present. (a) For a perfect lens, all incoming light rays get focused to a single point. (b) The Airy diffraction pattern corresponding to a point source that has been imaged by a perfect lens consists of a bright central spot surrounded by faint concentric rings. (c) For a real lens, light incident on the edges of a lens is refracted more than the light striking the center of the lens, and thus, there is not one unique focal point for all incident light rays. (d) Spherical aberration degrades resolution by redistributing some of the light from the central bright spot to the surrounding concentric rings.
Coma, or comatic aberration, is an image-degrading aberration associated with object points that are even slightly off axis. When an off-axis bundle of light is incident on a lens, the light will undergo different amounts of refraction depending on where it strikes the lens [see Figure 4.2 (a)]; as a result, each annulus of light will focus onto the image plane at a slightly different height and with a different spot size [see Figure 4.2 (b)], thereby leading to different transverse magnifications. The resulting image of a point source, which is shown in Figure 4.2 (c), is a complicated asymmetrical diffraction pattern with a bright central core and a triangular flare that departs drastically from the classical Airy pattern shown in Figure 4.1 (b). The elongated comet-like structure from which this type of aberration takes its name can extend either towards or away from the optical axis depending on whether the comatic aberration is negative or positive, respectively. Due to the asymmetry that coma causes in images, many consider it to be the worst type of aberration.
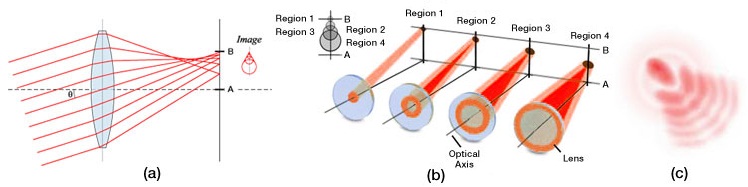
Figure 4.2 The effects of positive coma are shown. (a) When a light source is off-axis, the various portions of the lens do not refract the light to the same point on the image plane. (b) The central region of the lens forms a point image at the vertex of the cone, while larger rings on the periphery of the lens correspond to larger comatic circles that are displaced farther from the principal axis. (c) Coma leads to a complicated asymmetrical comet-like diffraction pattern characterized by an elongated structure of blotches and arcs. Note that the diffraction pattern shown assumes no spherical aberration.
Astigmatism, like coma, is an aberration that arises when an object point is moved away from the optical axis. Under such conditions, the incident cone of light will strike the lens obliquely, leading to a refracted wavefront characterized by two principal curvatures that ultimately determine two different focal image points. Figure 4.3 (a) shows the two planes one needs to consider: the tangential (also known as the meridional) plane and the sagittal plane; the tangential plane is defined by the chief ray (i.e., the light ray from the object that passes through the center of the lens) and the optical axis, while the sagittal plane is a plane that contains the chief ray and is perpendicular to the tangential plane. In addition to the chief light ray, Figure 4.3 (a) also shows two other off-axis light rays, one passing through the tangential plane and the other passing through the sagittal plane. For complex multi-element lens systems (e.g., microscope objective or ASOM system), the tangential plane remains coherent from one end of the system to the other while the sagittal plane usually changes slope as the chief ray’s propagation direction is altered by the various components in the lens system. Consequently, in general, the focal lengths associated with these planes will be different [see Figure 4.3 (b)]. If the sagittal focus and the tangential focal points are coincident, then the object point is on axis and the lens is free of astigmatism. However, as the amount of astigmatism present increases, the distance between these two foci will also increase, and as a result, the image will lose definition around its edges. The presence of astigmatism will cause the ideal circular point image to be blurred into a complicated elongated diffraction pattern that appears more linelike when more astigmatism is present [see Figures 4.3 (c) and 4.3 (d)].
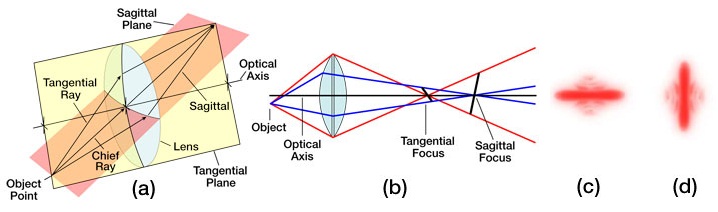
Figure 4.3 The effects of astigmatism, assuming the absence of spherical aberration and coma, are illustrated. (a) The tangential and sagittal planes are shown. (b) Light rays in the tangential and sagittal planes are refracted differently, ultimately leading to two different focal planes, which are labeled as the tangential focus and sagittal focus. (c) The Airy diffraction pattern of a point source as viewed at the tangential focal plane. (d) The Airy diffraction pattern of a point source as viewed at the sagittal focal plane.
For most optical systems, the final image must be formed on a planar surface; however, in actuality, a lens that is free of all other off-axis aberrations creates an image on a curved surface known as a Petzval surface. This nominal curvature of this surface, which is known as the Petzval curvature, is the reciprocal of the lens radius. For a positive lens, this surface curves inward towards the object plane, whereas for a negative lens, the surface curves away from that plane. The field curvature aberration arises from forcing a naturally curved image surface into a flat one. For the image, the presence of field curvature makes it impossible to have both the edges and central region of the image be crisp simultaneously. If the focal plate is shifted to the vertex of the Petzval surface [Position A in Figure 4.4 (a)], the central part of the image will be in focus while the outer portion of the image will be blurred, making it impossible to distinguish minor structural details in this outer region. Alternatively, if the image plane is moved to the edges of the Petzval surface [Position B in Figure 4.4 (a)], the opposite effect occurs; the edges of the image will come into focus, but the central region will become blurred. The best compromise between these two extremes is to place the image plane somewhere in between the vertex and edges of the Petzval surface, but regardless of its location, the image will never appear sharp and crisp over the entire field of view.
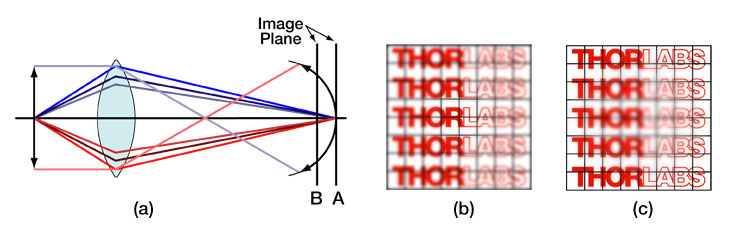
Figure 4.4 Field curvature, an aberration associated with off-axis objects, arises because the best image is not formed on the paraxial image plane but on a parabolic surface called the Petzval surface. (a) Depending on the location of the focal plane along the optic axis, either the central (if at location A) or peripheral (if at location B) portions of the field of view will be in focus but not both. (b) The central portion of the image will be crisp if the image plane is located at position A. (c) The edges of the image will be sharply in focus if the image plane is located at position B.
The last of the Seidel aberrations is distortion, which is easily recognized in the absence of all other monochromatic aberrations because it deforms the entire image even though each point is sharply focused. Distortion arises because different areas of the lens usually have different focal lengths and magnifications. If no distortion is present in a lens system, the image will be a true magnified reproduction of the object [see Figure 4.5 (b)]. However, when distortion is present, off-axis points are imaged either at a distance greater than normal or less than normal, leading to a pincushion [see Figure 4.5 (a)] or barrel [see Figure 4.5 (c)] shape, respectively.
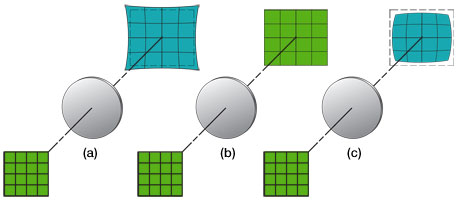
Figure 4.5 The effects of distortion, assuming the absence of all other forms of aberration, are illustrated. (a) Positive or pincushion distortion occurs when the transverse magnification of a lens increases with the axial distance; this effect causes each image point to be displaced radially outward from the center, with the most distant points undergoing the largest displacements. (b) If no distortion is present, the image will be a scaled duplicate of the object. (c) Negative or barrel distortion occurs when the transverse magnification of a lens decreases with axial distance; in this case, each image point moves radially inward toward the center; again, the most distant points undergo the largest displacements.
Chromatic Aberrations
The monochromatic aberrations discussed above can all be compensated for using a deformable mirror such as the one included in these adaptive optics kits. However, when a broadband light source is used, chromatic aberrations will result. Since a DM cannot compensate for these aberrations, we will only briefly mention them here. Chromatic aberrations, which come in two forms (i.e., lateral and longitudinal), arise from the variation of the index of refraction of a lens with incident wavelength. Since blue light is refracted more than red light, the lens is not capable of focusing all colors to the same focal point; therefore, the image size and focal point for each color will be slightly different, leading to an image that is surrounded by a halo. Generally, since the eye is most sensitive to the green part of the spectrum, the tendency is to focus the lens for that region; if the image plane is then moved towards (away from) the lens, the periphery of the blurred image will be tinted red (blue).
Introduction:
Adaptive optics (AO) is a rapidly growing multidisciplinary field encompassing physics, chemistry, electronics, and computer science. AO systems are used to correct (shape) the wavefront of a beam of light. Historically, these systems have their roots in the international astronomy and US defense communities. Astronomers realized that if they could compensate for the aberrations caused by atmospheric turbulence, they would be able to generate high resolution astronomical images; with sharper images comes an additional gain in contrast, which is also advantageous for astronomers since it means that they can detect fainter objects that would otherwise go unnoticed. While astronomers were trying to overcome the blurring effects of atmospheric turbulence, defense contractors were interested in ensuring that photons from their high-power lasers would be correctly pointed so as to destroy strategic targets. More recently, due to advancements in the sophistication and simplicity of AO components, researchers have utilized these systems to make breakthroughs in the areas of femtosecond pulse shaping, microscopy, laser communication, vision correction, and retinal imaging. Although dramatically different fields, all of these areas benefit from an AO system due to undesirable time-varying effects.
Typically, an AO system is comprised from three components: (1) a wavefront sensor, which measures these wavefront deviations, (2) a deformable mirror, which can change shape in order to modify a highly distorted optical wavefront, and (3) real-time control software, which uses the information collected by the wavefront sensor to calculate the appropriate shape that the deformable mirror should assume in order to compensate for the distorted wavefront. Together, these three components operate in a closed-loop fashion. By this, we mean that any changes caused by the AO system can also be detected by that system. In principle, this closed-loop system is fundamentally simple; it measures the phase as a function of the position of the optical wavefront under consideration, determines its aberration, computes a correction, reshapes the deformable mirror, observes the consequence of that correction, and then repeats this process over and over again as necessary if the phase aberration varies with time. Via this procedure, the AO system is able to improve optical resolution of an image by removing aberrations from the wavefront of the light being imaged.
The Wavefront Sensor:
The role of the wavefront sensor in an adaptive optics system is to measure the wavefront deviations from a reference wavefront. There are three basic configurations of wavefront sensors available: Shack-Hartmann wavefront sensors, shearing interferometers, and curvature sensors. Each has its own advantages in terms of noise, accuracy, sensitivity, and ease of interfacing it with the control software and deformable mirror. Of these, the Shack-Hartmann wavefront sensor has been the most widely used.
A Shack-Hartmann wavefront sensor uses a lenslet array to divide an incoming beam into a bunch of smaller beams, each of which is imaged onto a CCD camera, which is placed at the focal plane of the lenslet array. If a uniform plane wave is incident on a Shack-Hartmann wavefront sensor (refer to Figure 5A), a focused spot is formed along the optical axis of each lenslet, yielding a regularly spaced grid of spots in the focal plane. However, if a distorted wavefront (i.e., any non-flat wavefront) is used, the focal spots will be displaced from the optical axis of each lenslet. The amount of shift of each spot’s centroid is proportional to the local slope (i.e., tilt) of the wavefront at the location of that lenslet. The wavefront phase can then be reconstructed (within a constant) from the spot displacement information obtained (see Figure 5B).

Figure 5A When a planar wavefront is incident on the Shack-Hartmann wavefront sensor's microlens array, the light imaged on the CCD sensor will display a regularly spaced grid of spots. If, however, the wavefront is aberrated, individual spots will be displaced from the optical axis of each lenslet; if the displacement is large enough, the image spot may even appear to be missing. This information is used to calculate the shape of the wavefront that was incident on the microlens array.

Figure 5B Two Shack-Hartmann wavefront sensor screen captures are shown: the spot field (left-hand frame) and the calculated wavefront based on that spot field information (right-hand frame).
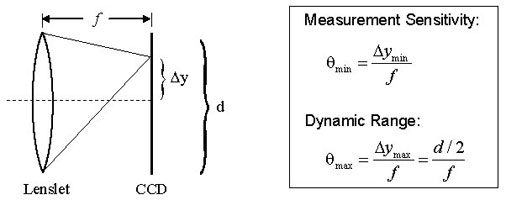
Figure 5C Dynamic range and measurement sensitivity are competing properties of a Shack-Hartmann wavefront sensor. Here, f, Δy, and d represent the focal length of the lenslet, the spot displacement, and the lenslet diameter, respectively. The equations provided for the measurement sensitivity θ min and the dynamic range θmax are obtained using the small angle approximation. θmin is the minimum wavefront slope that can be measured by the wavefront sensor. The minimum detectable spot displacement Δymin depends on the pixel size of the photodetector, the accuracy of the centroid algorithm, and the signal to noise ratio of the sensor. θmax is the maximum wavefront slope that can be measured by the wavefront sensor and corresponds to a spot displacement of Δymax, which is equal to half of the lenslet diameter. Therefore, increasing the sensitivity will decrease the dynamic range and vice versa.
The four parameters that greatly affect the performance of a given Shack-Hartmann wavefront sensor are the number of lenslets (or lenslet diameter, which typically ranges from ~100 - 600 μm), dynamic range, measurement sensitivity, and the focal length of the lenslet array (typical values range from a few millimeters to about 30 mm). The number of lenslets restricts the maximum number of Zernike coefficients that a reconstruction algorithm can reliably calculate; studies have found that the maximum number of coefficients that can be used to represent the original wavefront is approximately the same as the number of lenslets. When selecting the number of lenslets needed, one must take into account the amount of distortion s/he is trying to model (i.e., how many Zernike coefficients are needed to effectively represent the true wave aberration). When it comes to measurement sensitivity θmin and dynamic range θmax, these are competing specifications (see Figure 5C). The former determines the minimum phase that can be detected while the latter determines the maximum phase that can be measured.
A Shack-Hartmann sensor’s measurement accuracy (i.e., the minimum wavefront slope that can be measured reliably) depends on its ability to precisely measure the displacement of a focused spot with respect to a reference position, which is located along the optical axis of the lenslet. A conventional algorithm will fail to determine the correct centroid of a spot if it partially overlaps another spot or if the focal spot of a lenslet falls outside of the area of the sensor assigned to detect it (i.e., spot crossover). Special algorithms can be implemented to overcome these problems, but they limit the dynamic range of the sensor (i.e., the maximum wavefront slope that can be measured reliably). The dynamic range of a system can be increased by using a lenslet with either a larger diameter or a shorter focal length. However, the lenslet diameter is tied to the needed number of Zernike coefficients; therefore, the only other way to increase the dynamic range is to shorten the focal length of the lenslet, but this in turn, decreases the measurement sensitivity. Ideally, choose the longest focal length lens that meets both the dynamic range and measurement sensitivity requirements.
The Shack-Hartmann wavefront sensor is capable of providing information about the intensity profile as well as the calculated wavefront. Be careful not to confuse these. The left-hand frame of Figure 5D shows a sample intensity profile, whereas the right-hand frame shows the corresponding wavefront profile. It is possible to obtain the same intensity profile from various wavefunction distributions.
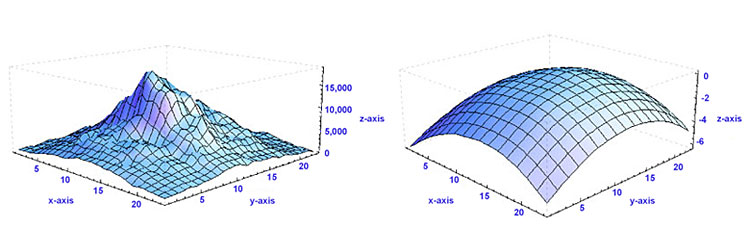
Figure 5D Several pieces of information are provided by the Shack-Hartmann wavefront sensor, including information about the total power at each lenslet and the calculated wavefront distribution present. Here, the left-hand frame shows a sample intensity profile, while the right-hand frame shows the corresponding wavefront.
The Deformable Mirror:
The deformable mirror (DM) changes shape in response to position commands in order to compensate for the aberrations measured by the Shack-Hartmann wavefront sensor (refer to the Aberrations tab to learn more about the aberrations that the DM can correct). Ideally, it will assume a surface shape that is conjugate to the aberration profile (see Figure 5E). In many cases, the surface profile is controlled by an underlying array of actuators that move in and out in response to an applied voltage. Deformable mirrors come in several different varieties, but the two most popular categories are segmented and continuous (see Figure 5F). Segmented mirrors are comprised from individual flat segments that can either move up and down (if each segment is controlled by just one actuator) or have tip, tilt, and piston motion (if each segment is controlled by three actuators). These mirrors are typically used in holography and for spatial light modulators. Advantages of this configuration include the ability to manufacture the segments to tight tolerances, the elimination of coupling between adjacent segments of the DM since each acts independently, and the number of degrees of freedom per segment. However, on the down side, the regularly spaced gaps between the segments act like a diffraction pattern, thereby introducing diffractive modes into the beam. In addition, segmented mirrors require more actuators than continuous mirrors to compensate for a given incoming distorted wavefront. To address the optical problems with segmented DMs, continuous faceplate DMs (such as those included in our AO Kits) were fabricated. They offer a higher fill factor (i.e., the percentage of the mirror that is actually reflective) than their segmented counterparts. However, their drawback is that the actuators are mechanically coupled. Therefore, when one actuator moves, there is some finite response along the entire surface of the mirror. The 2D shape of the surface caused by displacing one actuator is called the influence function for that actuator. Typically, adjacent actuators of a continuous DM are displaced by 10-20% of the actuation height; this percentage is known as the actuator coupling. Note that segmented DMs exhibit zero coupling but that isn’t necessarily desirable.

Figure 5E The aberration compensation capabilities of a flat and MEMS deformable mirror are compared. (a) If an unaberrated wavefront is incident on a flat mirror surface, the reflected wavefront will remain unaberrated. (b) A flat mirror is not able to compensate for any deformations in the wavefront; therefore, an incoming highly aberrated wavefront will retain its aberrations upon reflection. (c) A MEMS deformable mirror is able to modify its surface profile to compensate for aberrations; the DM assumes the appropriate conjugate shape to modify the highly aberrated incident wavefront so that it is unaberrated upon reflection.

Figure 5F Cross sectional schematics of the main components of BMC's continuous (left) and segmented (right) MEMS deformable mirrors.
The range of wavefronts that can be corrected by a particular DM is limited by the actuator stroke and resolution, the number and distribution of actuators, and the model used to determine the appropriate control signals for the DM; the first two are physical limitations of the DM itself, whereas the last one is a limitation of the control software. The actuator stroke is another term for the dynamic range (i.e., the maximum displacement) of the DM actuators and is typically measured in microns. Inadequate actuator stroke leads to poor performance and can prevent the convergence of the control loop. The number of actuators determines the number of degrees of freedom that the mirror can correct for. Although many different actuator arrays have been proposed, including square, triangular, and hexagonal, most DMs are built with square actuator arrays, which are easy to position on a Cartesian coordinate system and map easily to the square detector arrays on the wavefront sensors. To fit the square array on a circular aperture, the corner actuators are sometimes removed. Although more actuators can be placed within a given area using some of the other configurations, the additional fabrication complexity usually does not warrant that choice.

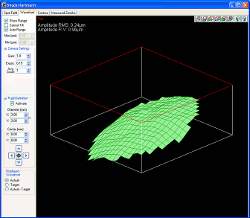
Figure 5G A cross-like pattern is created on the DM surface by applying the voltages necessary for maximum deflection of the 44 actuators that comprise the middle two rows and middle two columns of the array. The frame on the left shows a screen shot of the AO kit software depicting the DM surface, whereas the frame on the right, which was obtained through quasi-dark field illumination, shows the actual DM surface when programmed to these settings. Note that the white light source used for illumination is visible in the lower right-hand corner of the photograph.
Figure 5G (left frame) shows a screen shot of a cross formed on the 12 x 12 actuator array of the DM included with the adaptive optics kit. To create this screen shot, the voltages applied to the middle two rows and middle two columns of actuators were set to cause full deflection of the mirror membrane. In addition to the software screen shot depicting the DM surface, quasi-dark field illumination was used to obtain a photograph of the actual DM surface when programmed to these settings (see Figure 5G, right frame)
The Control Software:
In an adaptive optics setup, the control software is the vital link between the wavefront sensor and the deformable mirror. It converts the wavefront sensor’s electrical signals, which are proportional to the slope of the wavefront, into compensating voltage commands that are sent to each actuator of the DM. The closed-loop bandwidth of the adaptive optics system is directly related to the speed and accuracy with which this computation is done, but in general, these calculations must occur on a shorter time scale than the aberration fluctuations.
In essence, the control software uses the spot field deviations to reconstructs the phase of the beam (in this case, using Zernike polynomials) and then sends conjugate commands to the DM. A least-squares fitting routine is applied to the calculated wavefront phase in order to determine the effective Zernike polynomial data outputted for the end user. Although not the only form possible, Zernike polynomials provide a unique and convenient way to describe the phase of a beam. These polynomials form an orthogonal basis set over a unit circle with different terms representing the amount of focus, tilt, astigmatism, comma, et cetera; the polynomials are normalized so that the maximum of each term (except the piston term) is +1, the minimum is –1, and the average over the surface is always zero. Furthermore, no two aberrations ever add up to a third, thereby leaving no doubt about the type of aberration that is present.
| Posted Comments: | |
user
(posted 2024-02-21 18:18:39.57) We need a mirror file named "BMC Multi DM v4.mir" for a multi DM bought in 2015. Please sent it to us. ksosnowski
(posted 2024-02-22 04:27:16.0) Thank you for requesting this file from us. The necessity of this stems from using new AOkit software with an old device (2015). Rather than this approach, we have sent you the old software for your 2015 AOkit. Because of this approach, the file you request here was not required, and your system has been confirmed to be working. For newer mirrors, BMC has recently started a database for the modern formats of mirror files which can be accessed here for use with our current AOkit software: https://bostonmicromachines.com/customer-files/ user
(posted 2023-11-08 17:10:07.873) Hello, I am using this multi-driver with deformable mirror, and the input range of this DM is from 0 to 1 in the software. I could connet this DM and control it using Matlab. If I provide a command greater than 1, like 1.5 or 2, what would happen to DM? Is it still safe? or does it damage the DM? cdolbashian
(posted 2023-11-15 03:57:19.0) Thank you for reaching out to us with this inquiry. Looking into the documentation within the manual, we see that the 0 and 1 correspond to the minimum and maximum stroke respectively. Increasing the value beyond this will not increase the actuator's stroke. I have contacted you directly to inquire after your application and the need for such an input. USER A
(posted 2023-07-18 12:32:24.85) hi, I wonder which parameter determines the accuracy of modifying the wavefront? Is the Surface Quality? cdolbashian
(posted 2023-08-04 12:27:18.0) Thank you for reaching out to us with this inquiry. Surface quality surely contributes, but accuracy of piezo-electric actuator position is also a key factor, as this is what distorts/corrects the wavefront. I have reached out to you directly to discuss your application. For all other performance specs, please see the "specs" tab above. marcotronixs
(posted 2016-04-01 17:24:02.623) hello good afternoon, just to see if they could send me a copy of a DM software kit that makes adaptive optics buy time with you. The UM01 AOKI kt is the name of the Autonomous University of Puebla Mexico City besembeson
(posted 2016-04-05 09:09:57.0) Response from Bweh at Thorlabs USA: Yes we can send the software to you. I will contact you. ilitivn
(posted 2015-12-14 04:59:50.34) Good day.
Can you send me a price for your Deformable Mirrors?
Thanks.
Igor. jlow
(posted 2015-12-14 11:14:47.0) Response from Jeremy at Thorlabs: The latest price is listed on the website for the deformable mirror system. To request a quote, you can contact us directly at sales@thorlabs.com. rscholl
(posted 2013-01-03 14:31:00.0) Response from Ryan at Thorlabs: We do not believe our deformable mirror is fast enough to provide the spatial incoherence required by your application. Other things you might consider could be: (1) guiding the light through a multimode fiber resting on a vibrating surface, (2) a second diffuser rotating in the opposite direction of the first, or (3) an integrating sphere with an input and output port following your rotating diffuser. I also contacted you by email. madhavi.krishnan
(posted 2012-11-25 10:28:09.293) Hello, I am interested in distorting a planar wavefront at > 10 kHz in order to destroy the spatial coherence in the beam for an interferometric application. I was looking at the SLMs here as a way of doing that, but the less expensive 6x6 may not be fast enough for what we want to do. The faster one may be an overkill since we do not need a programmable distortion. Could you suggest another optical component, perhaps electro-optic or acousto-optic that might deliver spatial distortion of the wavefront at high speeds. Essentially I am looking for the same effect on the beam as that produced by a rotating ground glass diffuser, just orders of magnitude faster than the mechanical. Any input would be highly appreciated.
Thanks and best wishes, Madhavi jlow
(posted 2012-09-26 14:57:00.0) Response from Jeremy at Thorlabs: The actuator stroke is the maximum displacement of the DM actuators. user
(posted 2012-09-26 12:58:07.0) Hello, can you tell me what in your description "stroke" of the DM means...is it the stroke between 2 adjacent actuators or for the whole DM area? Sincerely Yours, Thomas tcohen
(posted 2012-04-13 11:20:00.0) Response from Tim at Thorlabs: Peak power for a CW beam is about 200W/cm^2. Note that this is based off of measurements taken at 1550nm. As for the Shack-Hartmann Wavefront Sensor, the max power will depend on the wavefront curvature. The flatter the wavefront, the smaller the focus size of the spots on the camera, and thus the higher the power density on those spots. Typically a power of a few 10's µW spread over the whole sensor area will give you a good SNR. For a flat wavefront, 1mW will already saturate the sensor. Lehmann
(posted 2012-04-12 19:07:34.0) I would like to know the maximum power at 1.06 um I can put on your deformable mirrors. I would also like to know how much power I would have to put into the Shack-Hartman Wavefront sensor. If I purchase a pair user
(posted 2010-08-17 06:25:36.0) Please, put "mirror, driver and software included" down by the price box.
From Alex user
(posted 2010-06-02 23:14:46.0) Response from Javier at Thorlabs to nssycit: we can send you the manual for the AO Kit, which contains useful information regarding setup, alignment, and software (It is also available here: http://www.thorlabs.com/NewGroupPage9.cfm?ObjectGroup_ID=3208). We can gladly assist you if you have particular questions. nssycit
(posted 2010-06-02 21:11:09.0) Hello
I have downloaded the wavefront sensor control softwear, and I want to kown more about AO systems and deformable mirrors softwares, but your company doesnt have these for downloading. So I want to kown how I can get these control softwares befor I purchase these products. thanks much.
Best wishes! jjurado
(posted 2010-06-01 21:06:58.0) Response from Javier at Thorlabs to nssycit: AR stands for anti-reflective. The protective window use in the deformable mirrors is coated with a broadband anti-reflective coating with low reflectivity in the 400-1100 range (see Graphs tab). nssycit
(posted 2010-06-01 17:24:32.0) in “Products Home >> Adaptive Optics >> Deformable Mirrors>> overview >> features >> Protective Window with 6o Wedge and Broadband AR Coating (400 - 1100 nm)" what does the iterm AR stand for? |

Figure 7.1 DM Electrical Interface
Considerations
Ideally, the deformable mirror needs to assume a surface shape that is complementary to, but half the amplitude of, the aberration profile in order to compensate for the aberrations and yield a flat wavefront. However, the actual range of wavefronts that can be corrected by a particular deformable mirror is limited by several factors:
- Actuator stroke is another term for the dynamic range (i.e., the maximum displacement) of the deformable mirror actuators and is typically measured in microns. Inadequate actuator stroke leads to poor performance by limiting aberration amplitudes that may be compensated, preventing the convergence of the control loop.
- The number of actuators limits the degrees of freedom of the wavefront control system, and therefore the complexity of the wavefront that may be corrected.
- The speed of the deformable mirror is important if you are trying to correct for rapidly changing wavefronts. For mirrors that exhibit hysteresis (i.e., piezoelectric deformable mirrors), the control software will need to calculate the correct voltage changes to produce the desired mirror displacement, which can lower the mirror speed.
- Optical power handling will also vary depending on the mirror coating and actuator design. For our mirrors, the piezoelectric deformable mirrors have significantly higher power handling than the MEMS systems [up to 1 J/cm² (1064 nm, 10 ns, 10 Hz, Ø10 mm) for the protected silver coated versions]. They can also be custom coated to operate inside laser cavities (contact Tech Support for details).
- Hysteresis in piezoelectric deformable mirrors means that the displacement of a mirror segment at a given voltage is different if that voltage is approached from a higher voltage compared to a lower voltage. Our piezoelectric deformable mirrors offer hysteresis compensation when used with Thorlabs' control software, while the MEMS-based deformable mirrors are inherently hysteresis-free. The hysteresis compensation for the piezoelectric deformable mirrors can be turned off when operating the mirror with open-loop control, which can increase the speed.
The first four considerations are physical limitations of the deformable mirror itself, whereas hysteresis may be a limitation of the control software and/or a physical limitation of the mirror itself. Additionally, the wavelength range of the deformable mirror coating and any protective windows installed in the mirror head must be appropriate for the application wavelength.
Comparison
Thorlabs' piezoelectric deformable mirrors provide a larger stroke, and therefore are able to correct for larger wavefront deviations, than our MEMS-based deformable mirrors. However, they contain a lower density of actuators over the active area of the mirror than the MEMS-based Multi DMs below, which means they cannot correct wavefront deviations on as fine of a spatial scale as the MEMS-based DMs.
To correct for both large amplitude and small spatial scale wavefront distortions, consider using a piezoelectric and MEMS-based deformable mirror in tandem, typically referred to in the literature as a woofer-tweeter configuration. The piezoelectric deformable mirror can correct for the tip, tilt, and lower order (lower spatial frequency) wavefront distortions, while the MEMS-based device compensates for higher order (higher spatial frequency) wavefront distortions. In nature, lower order wavefront distortions typically have larger magnitudes than do higher order wavefront distortions. Therefore, the combination of our lower actuator count, larger displacement, piezo-based DM and the higher actuator count, smaller displacement, MEMS-based DM is well suited to be used in a woofer-tweeter configuration.
| Deformable Mirror Comparison | |||||||
|---|---|---|---|---|---|---|---|
| Deformable Mirror Type |
MEMS-Based from Boston Micromachines | Piezoelectric | |||||
| Item # | DM140A-35-UP01 | DM140A-35-P01 | DM140A-35-UM01 | DMP40-F01 DMP40/M-F01 |
DMP40-P01 DMP40/M-P01 |
DMH40-F01 DMH40/M-F01 |
DMH40-P01 DMH40/M-P01 |
| Actuator Array | 140 Actuators in a 12 x 12 Array | 40 Piezoceramic Disk Segments in a Circular Keystone Array (Elements 1 - 24 Inside Pupil Diameter, Elements 25 - 40 Outside Pupil Diameter) |
|||||
| Actuator Stroke | 3.5 µm per Actuator | Defocusa: ±6.5 µm Astigmatisma: ±6.8 µm Comaa: ±2.5 µm Trefoila: ±2.4 µm Tetrafoila: ±2.1 µm Secondary Astigmatisma: ±1.1 µm Third Order Spherical Aberrationa: ±1.0 µm |
Defocusa: ±17.6 µm Astigmatisma: ±18.4 µm Comaa: ±6.8 µm Trefoila: ±6.5 µm Tetrafoila: ±5.7 µm Secondary Astigmatisma: ±3.0 µm Third Order Spherical Aberrationa: ±2.7 µm |
||||
| Tip/Tilt | N/A | 3 Spiral Arms for ±2.0 mrad of Tip/Tilt | N/A | ||||
| Pupil Dimensions | 4.4 mm x 4.4 mm | Ø10.0 mm | Ø14.0 mm | ||||
| Mirror Coating (Click for Plot) |
Aluminum | Protected Silver | Gold | UV-Enhanced Aluminum |
Protected Silver | UV-Enhanced Aluminum |
Protected Silver |
| Mirror Wavelength Range |
400 - 1100 nm | 400 - 1100 nm | 600 - 1100 nm | 250 - 450 nm (Ravg > 89%) |
450 nm - 2 µm (Ravg > 97.5%), 2 - 20 µm (Ravg > 96%) |
250 - 450 nm (Ravg > 89%) |
450 nm - 2 µm (Ravg > 97.5%), 2 - 20 µm (Ravg > 96%) |
| Hysteresis | None | 15% Typical, 25% Max | 20% Typical, 25% Max | ||||
| Response Time | <100 µs (~3.5 kHz) Mechanical Response Time (10% - 90%) | 0.5 ms (Full Stroke) Mirror Response Time 5 ms (Full Stroke) Tip/Tilt Response Time |
0.5 ms (Full Stroke) Mirror Response Time | ||||
| Frame Rate (Max) | 8 kHz (34 kHz Bursts) | 4 kHz via USB 2.0 (Over Entire Voltage Range) | |||||
 Products Home
Products Home















 MEMS Deformable Mirrors
MEMS Deformable Mirrors